106. 从中序与后序遍历序列构造二叉树

leecode原题

题目

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例

示例 1:

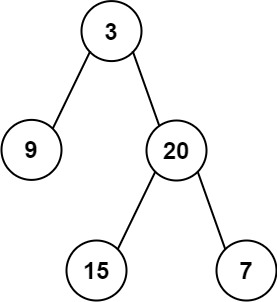
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示：

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

解题思路

思路

以后序数组的最后一个元素为切割点(后序数组的最后一个元素总是根节点)，找到该切割点在中序数组中的索引下标, 将中序和后序数组以切割点下标一分为二(这里要尤其主要边界)，然后一次以分割后的中序和后续数组的左半数组和右半数组依次作为左右子树进行递归构建。

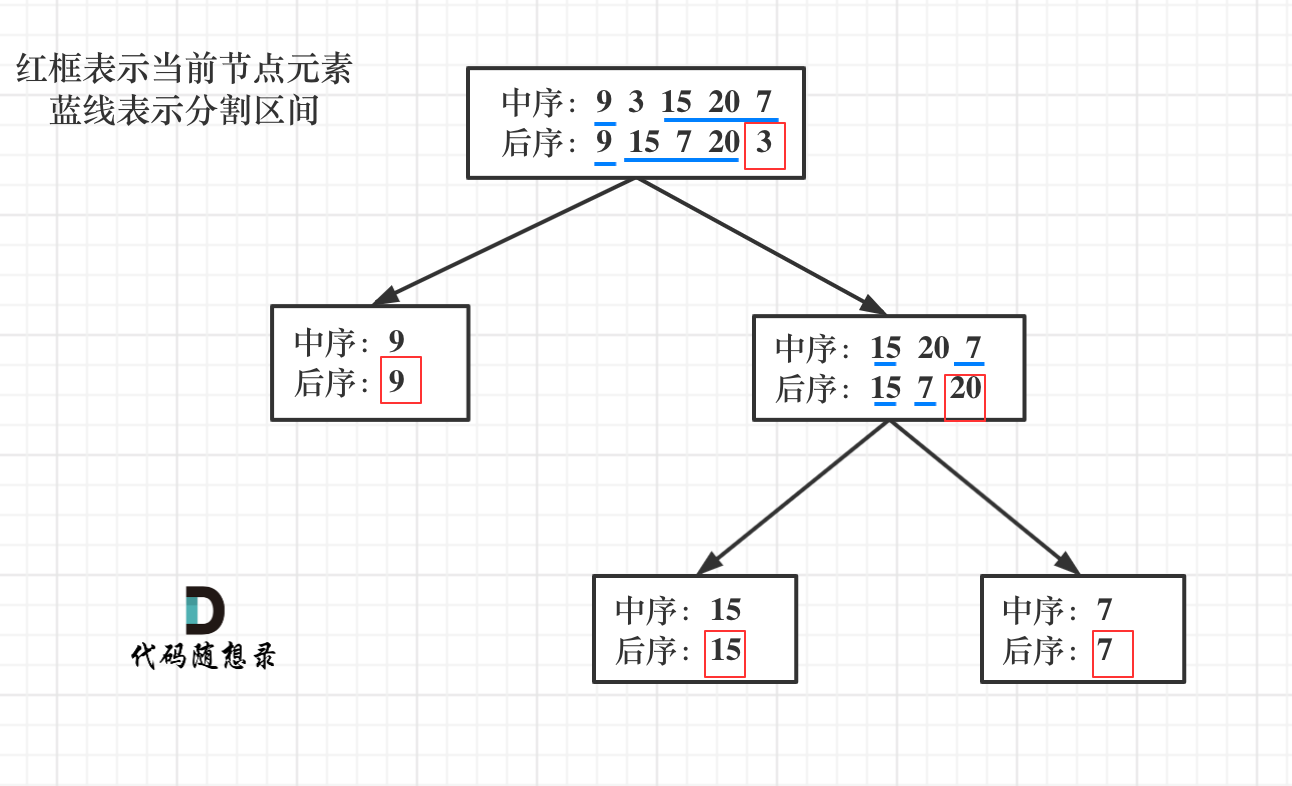
说到一层一层切割，就应该想到了递归。

来看一下一共分几步：

1. 第一步：如果数组大小为零的话，说明是空节点了。
2. 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
3. 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
4. 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
5. 第五步：切割后序数组，切成后序左数组和后序右数组
6. 第六步：递归处理左区间和右区间

实现

源码

func buildTree(inorder []int, postorder []int) *TreeNode {
    // 节点为空
    if len(inorder) == 0 || len(postorder) == 0 {
        return nil
    }
    // 找到后序数组最后一个元素(就是子树的根节点)在中序数组中的下标, 然后进行二分
    pos := findInorderPos(inorder, postorder[len(postorder)-1])
    // 这里一定要注意边界!!!
    root := &TreeNode{
        Left:  buildTree(inorder[:pos], postorder[:pos]),
        Right: buildTree(inorder[pos+1:], postorder[pos:len(postorder)-1]),
        Val:   inorder[pos],
    }
    return root
}

// 找中序目标值的索引位置
func findInorderPos(inorder []int, target int) int {
    for index, v := range inorder {
        if v == target {
            return index
        }
    }
    return -1
}