90. 子集 II

leecode原题

题目

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例

示例 1:

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2:

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10

解题思路

思路

这道题目和78-子集区别就是集合里有重复元素了，而且求取的子集要去重。

那么关于回溯算法中的去重问题，在40-组合总和II中已经详细讲解过了，和本题是一个套路。

用示例中的[1, 2, 2] 来举例，如图所示： （注意去重需要先对集合排序）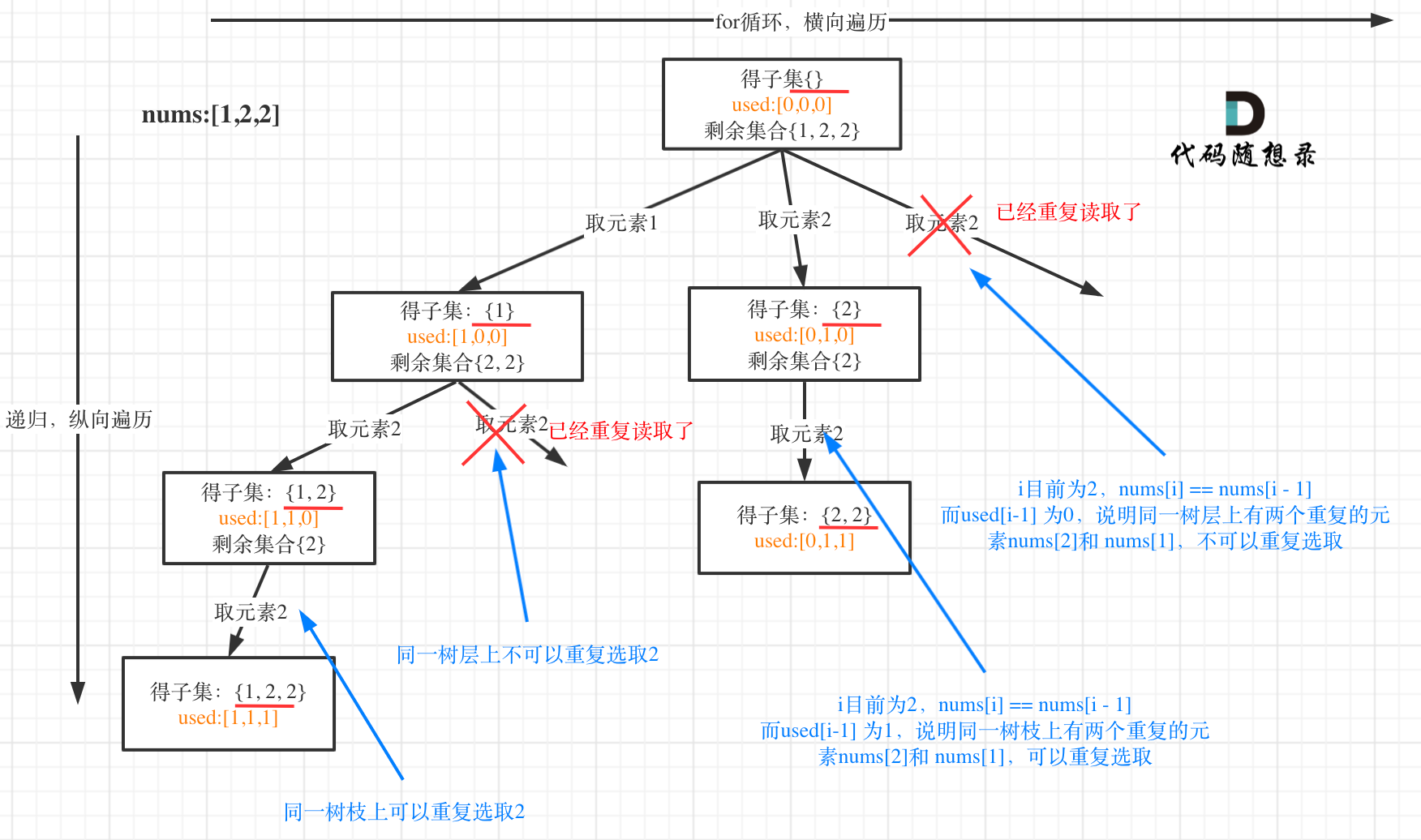

从图中可以看出，同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集！

实现

源码

var (
    res  = make([][]int, 0) // 存放最终结果
    path = make([]int, 0)   // 存放中间结果
    used = make([]bool, 0)  // 记录是否被使用
)

func backtracking(nums []int, startIndex int) {
    // 收集子集，要放在终止添加的上面，否则会漏掉自己
    temp := make([]int, len(path))
    copy(temp, path)
    res = append(res, temp)

    if startIndex >= len(nums) { // 可以不加, for循环会自动退出
        return
    }
    for i := startIndex; i < len(nums); i++ {
        // used[i - 1] == true，说明同一树枝nums[i - 1]使用过
        // used[i - 1] == false，说明同一树层nums[i - 1]使用过
        // 而我们要对同一树层使用过的元素进行跳过
        if i > 0 && nums[i] == nums[i-1] && used[i-1] == false {
            continue
        }
        path = append(path, nums[i])
        used[i] = true
        backtracking(nums, i+1)
        path = path[:len(path)-1]
        used[i] = false
    }
}

func subsetsWithDup(nums []int) [][]int {
    res = make([][]int, 0)
    path = make([]int, 0)
    used = make([]bool, len(nums))
    // 去重需要先排序
    sort.Ints(nums)
    backtracking(nums, 0)
    return res
}